
فهرست مطالب (با کلیک بر روی عنوان، مرور گر به سر خط مبحث مد نظر خواهد رفت):
۲- چگونگی استفاده از آماره دوربین واتسون
۲-۲- دامنه تغییرات دوربین واتسون و مقدار بهینه آن
۳- شرایط لازم برای اعتبار آزمون Durbin Watson
تشخیص خود همبستگی های مرتبه اول
۴- جدول مقادیر بحرانی آزمون دوربین-واتسن (DW) و نحوه استفاده
۵- اعتبار دوربین-واتسون وقتی متغیر وابسته با وقفه در مدل است
۶- چگونگی محاسبه دوربین واتسون در eviews
1- آزمون دوربین-واتسون چیست؟
آزمون دوربین واتسون (Durbin Watson) که به اختصار با DW نشان داده می شود، یک آزمون معروف و بسیار پر کاربرد آماری است که برای تشخیص خود همبستگی مرتبه اول باقیمانده ها یا جملات خطا در یک مدل رگرسیون به کار می رود.
این آزمون به صورت گسترده در نرم افزار ایویوز به کار می رود و ما در تمام مدلهایی که با eviews ران (اجرا) می کنیم، این آماره را مورد بررسی قرار می دهیم. بدین ترتیب که کنترل می کنیم این آماره در محدوده مجاز خود قرار داشته باشد، در غیر اینصورت به نامناسب بودن مدل برآورد شده پی می بریم.
با توجه به پیچیدگی مباحث ریاضی و فراری بودن خیلی ها از این قبیل مباحث، فرمول نحوه محاسبه این آزمون را در اینجا بیان نمی کنیم و به جای آن بر کاربرد این آزمون تمرکز می کنیم که از این آزمون چه استنباط و تحلیلی می توان بدست آورد و چه اقداماتی بعد از آن می بایست انجام داد (آموزش تحلیل آماره دوربین واتسون). این آزمون جزئیات مهم زیادی دارد ولی چنانچه خیلی سریع می خواهید بدانید با این آماره چه باید کرد، به بخش خلاصه در انتهای این مبحث مراجعه نمایید.
{برو به فهرست}
2- چگونگی استفاده از آماره دوربین واتسون
1-2- فرضیه ها:
برای این آزمون آماری، فرضیه های H0 و H1 به قرار زیر است:
H0 : عدم وجود خودهمبستگی بین جملات خطا
H1: وجود خودهمبستگی بین جملات خطا
توجه شود که خود همبستگی ذکر شده در اینجا بین زمان های t و t-1 می باشد. عدم خود همبستگی، یعنی خطاهای زمان t و t-1 از یکدیگر مستقل باشند.
2-2- دامنه تغییرات دوربین واتسون و مقدار بهینه آن:
فرمول آماره این آزمون به گونه ای است که
- اگر خود همبستگی جملات خطای مدل برابر صفر باشد، آنگاه مقدار این آماره برابر DW=2 خواهد شد. که هدف ما نیز همین است که مدلی برآورد کنیم که در آن جملات خطا هیچ خود همبستگی با یکدیگر نداشته باشند، بنابراین اگر در مدل خود دیدیم که این آماره برابر 2 بدست آمد، از بابت خودهمبستگی فکرمان آسوده خواهد بود.
- اگر خود همبستگی شدید و مثبت بین جملات خطا وجود داشته باشد، آنگاه مقدار این آماره برابر DW=0 خواهد شد. بنابراین مقدار کم دربین واتسون (حدودا کمتر از عدد 1.5) نشان دهنده وجود مشکل در مدل است و حاکی از خود همبستگی مثبت بین جملات خطا (یا باقیمانده ها) در مدل می باشد که باید برای رفع آن فکری بر داریم.
- اگر خود همبستگی شدید و منفی بین جملات خطا وجود داشته باشد، آنگاه مقدار این آماره برابر DW=4 خواهد شد. بنابراین مقدار زیاد دوربین واتسن (حدودا بیشتر از 2.5) نشان دهنده وجود مشکل در مدل بوده و خود همبستگی منفی بین جملات خطا را می رساند که اصلا مطلوب ما نیست. {برو به فهرست}
بنابراین همانگونه که ملاحظه نمودید، مقدار این آماره در بازه بین 0 تا 4 در نوسان است و مقدار بهینه آن برابر 2 می باشد. مقادیر کمتر یا بیشتر از 2 نشان دهنده وجود مساله در مدل است. حالا اینکه چقدر کمتر یا چقدر بیشتر از عدد 2 نشان دهنده مشکل است باید با توجه به جدول مقادیر بجرانی آزمون دوربین واتسون انجام پذیرد. این جدول در همین مبحث آمده است.
3- شرایط لازم برای اعتبار آزمون Durbin Watson
این آزمون دارای محدودیت هایی هنگام استفاده می باشد که می بایست با شناخت کامل این محدودیت ها به قضاوت در خصوص کیفیت مدل بپردازیم.
تشخیص خود همبستگی های مرتبه اول:
یکی از محدودیت های این آماره آزمون این است که فقط خود همبستگی بین مقادیر سال جاری و سال قبل (یا دوره جاری و دوره قبل) را در نظر می گیرد و در خصوص خود همبستگی های مرتبه بالاتر فاقد کارایی می باشد.
وجود جمله ثابت در مدل:
برای اعتبار داشتن آزمون DW باید جمله ثابت (همان c) در معادله رگرسیون باشد. {برو به فهرست}
شرایط دیگری نیز وجود دارد که به دلیل کم بودن کاربرد آنها، از آن صرف نظر می کنیم.
4- جدول مقادیر بحرانی آزمون دوربین-واتسن (DW) و نحوه استفاده
نتیجه آماره دوربین واتسون را نمی توان با مقادیر بحرانی توزیع های شناخته شده معروف مثل t و F مقایسه کرد. بلکه جدول جداگانه ای دارد.
1-4- چگونگی استفاده از جدول
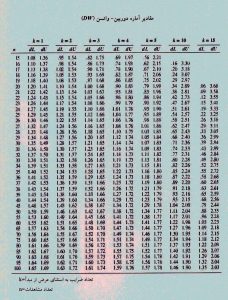
در جدول زیر می بایست با توجه به n که تعداد مشاهدات است و K تعداد ضرایب مدل رگرسیونی به استثنای عرض از مبدا می باشد، به مقادیر داخل جدول مراجعه نموده و دو عدد Du و Dl را یادداشت نمود.
آنگاه با توجه به نمودار زیر در خصوص رد یا عدم رد فرض H0 (در همین صفحه این فرض ها را تعریف نموده ایم) تصمیم می گیریم:
2-4- جدول مقادیر بحرانی DW
جدول ارزش های بحرانی یا مقادیر بحرانی آزمون دوربین واتسون، که برای تصمیم گیری در خصوص وجود یا عدم وجود خودهمبستگی جملات خطای رگرسیون به کار می رود، به قرار زیر است. برای مشاهده آن در اندازه بزرگتر روی آن کلیک نمایید:
3-4- مثال
مدلی را در نظر بگیرید که تعداد مشاهدات برای برآورد آن 50 و به غیر از ضریب ثابت (یا همان عرض از مبداء) دارای 4 ضریب (یا متغیر) می باشد. از خروجی نرم افزار ای ویوز مقدار آماره برابر DW=1.18 بدست آمده است. {برو به فهرست}
از جدول مقادیر بحرانی فوق نیز این اطلاعات را داریم:
Dl= 1.38
Du= 1.72
4 – Du = 2.28
4 – Dl = 2.62
تصمیم: از آنجایی که DW=1.18 کمتر از Dl= 1.38 است، بنابراین این مدل دارای خود همبستگی مثبت است و برای رفع آن باید فکری اندیشید. {برو به فهرست}
نکته
توجه شود که اگر متغیر وابسته تاخیری در مدل باشد، شیوه تصمیم گیری فوق تغییر خواهد نمود که در بخش بعدی به آن پرداخته ایم.
5- اعتبار دوربین-واتسون وقتی متغیر وابسته با وقفه در مدل است
وقتی در سمت راست مدل، متغیرهای با وقفه از متغیر وابسته وجود داشته باشد، استفاده از آزمون دوربین واتسون برای بررسی خودهمبستگی جملات خطا صحیح نیست و می بایست از آزمون های دیگری برای این کار استفاده کرد که مجال ذکر آن در اینجا نیست. {برو به فهرست}
چنانچه کار شما در این مرحله دچار مساله است، توضیحات محصول (شناسایی و رفع خود همبستگی سریالی) را در محصولی با همین نام در منو محصولات این سایت مطالعه نمایید و در صورتی که با شرایط شما تطبیق داشت این محصول آموزشی را خریداری نموده و استفاده نمایید.
6- چگونگی محاسبه دوربین واتسون در eviews
حال اینکه چطور با نرم افزار ایویوز آزمون دوربین واتسون را محاسبه کنیم. پاسخ آن سخت نیست. هر جا که شما نیاز به این آزمون برای تصمیم گیری داشته باشید، نرم افزار هوشمند ایویوز آنرا در هنگام اجرای مدل برای شما محاسبه می کند!
به عبارت دیگر وقتی معادله رگرسیونی یا مدلی با eviews برآورد می شود، همراه با نتایج برآورد ضرایب رگرسیون، این آماره نیز گزارش شده و در خروجی نرم افزار ای ویوز می آید.
تصمیم گیری قطعی با دوربین واتسون:
برای اینکه بتوانید قاطع در خصوص این آزمون در پایان نامه یا پژوهش خویش بنویسید، لازم است طبق بخش قبلی این مبحث، مقدار آماره را با اعداد مندرج در جدول مقادیر بحرانی مقایسه کنید.
خلاصه (مساله خود همبستگی جملات خطا)
از منظر اجرایی، کل مبحث بالا را می توان در دو خط زیر خلاصه نمود:
اگر آماره دوربین واتسون بدست آمده از خروجی eviews حول و حوش عدد 2 بود (به صورت تقریبی از 1.5 بیشتر و از 2.5 کمتر بود)، مدل شما از نظر عدم وجود خود همبستگی بین جملات خطا، که یکی از فروض اصلی مدل رگرسیونی است، مساله ای ندارد.






سلام، عدد دوربين واتسون من 2.66 بدست آمده که از 2.5 بيشتر است. احتمال دارد که این مشکل ,
از اشتباه واردشدنِ داده ها,,
باشد؟
معذرت میخوام.
چون این هفته باید مقاله ای ارسال کنم.
سلام. بله. داده ها را يک بررسي داشته باشيد. ممکن است به خاطر وجود چند داده پرت باشد. کلا قبل از هر گونه اقدامی در نرم افزار ای ویوز می بایست وضعیت داده های پرت بررسی شود. یکی دو داده پرت ممکن است سرنوشت مدل شما را تغییر داده باشد. آموزش ویدئویی شناسایی و برخورد با داده پرت:
https://www.eviews-iran.ir/product/outlier/
سلام بله شما میتونید با وارد کردar1یا ۲مشکل را رفع کنید
سلام
دقت داشته باشید که با وارد کردن ar(1) به مدل، عملا مدل رگرسیونی خود را به یک مدل پویا تبدیل کرده اید. درست است که مساله نرخ پایین دربین واتسون حل می شود اما مدل خود را عوض کرده و تغییر داده اید. گاه وقتی اساتید این راه حل را قبول نمی کنند، خصوصا در داده های پانل.
سلام,وقتتون بخیر.
مدل رگرسیونی من عرض از مبدا نداره,الان که ازمون دوربین-واتسون واسش معتبر نیست برای کنترل عدم همبستگی باقیمانده ها باید از چه روش یا آزمونی استفاده کنم؟
ممنون
سلام؛ حتی الامکان عرض از مبدا یا ضریب ثابت در مدل باشد. وجود عرض از مبدا در مدل باعث می شود که شرط برابر صفر بودن میانگین جملات خطا نیز خود به خود در مدل برقرار شود.
بهرحال اگر در مدل نیست، با بررسی نمودار سری زمانی باقیمانده (جملات خطا) علائم هم خطی را در نمودار کنترل کرد. به این صورت که اگر جملات خطا دارای خود همبستگی باشند، در طول زمان به طور منظم تغییر می کنند. در صورتی که بایستی تغییرات آنها کاملا تصادفی باشد.
ممنون از راهنماییتون
سلام خسته نباشید
مدل من پانل آستانه بود ولی تعداد متغیرهام کم بودش و استاد داور این ایراد که باید آزمون کفایت مدل رو اجرا کنم رو از من گرفتن توضیحیی هم که دادن این بودش که من باید جمله خطای مدل نهایی را بدست بیارم و کلوگرام آن را رسم کنم و آزمون تشخیص خودهمبستگی با استفاده از رسم اجزای اخلال هستش در واقع خواستم ازتون درباره رسم این کلوگرام بپرسم که به چه نحوی هستش؟
سلام
خدمت شما عرض کنم که به طور کلي در هر مدلي با استفاده از نرم افزار ايويوز مي توان باقيمانده ها را به راحتي استخراج نمود و بر روي آن به صورت جداگانه آزمون ها و بررسی هاي لازم را اجرا نمود. وقتي مدلي را اجرا مي کنيد به طور اتوماتيک باقيمانده ها يا جملات اخلال اين مدل در متغير resid در نرم افزار ايويوز ذخيره مي شود. حال شما مي توانيد کرولوگرام (correlogram ) آنرا ترسيم نماييد تا ببينيد که وضعيت باقيمانده ها به چه صورت است. کرولوگرام يا correlogram از ابزارهاي اوليه بررسي و تشخيص مدل در مبحث سريهاي زماني است و با نگاهي به آن مي توانيد خود همبستگي و خودهمبستگي جزئي را در سري زماني تشخيص دهيد. یک مدل خوب مدلی است که کرولوگرام باقیمانده های آن هیچ نوع خود همبستگی را نشان ندهد.
براي ترسيم آن هم کافي است پس از اجراي مدل به سراغ متغير resid برويد و روي آن کليک کنيد. در منوي ويو دستور کرولوگرام به چشم مي خورد.
با سلام مجدد
بسیار ممنونم از راهنمایی خوب و کاملتون استاد عزیز من کرولوگرام رو رسم کردم فقط اینکه خواستم بپرسم نحوه تحلیل AC و PAC و Q-STATE و PROB به چه صورت هست؟ ممنون میشم که اگر توضیحی درباره نحوه تحلیل هم ارائه کنید.
درواقع تحلیل معنادار بودن و معنادار نبودن به چه صورت هست
خواهش. تحلیل کامل AC و PAC مبحث نسبتا مفصلی است که در مباحث سری های زمانی در اقتصاد سنجی گنجانده شده است. منتها اینگونه به شما بگویم که یک سری از باقیمانده های مدل نباید هیچ حرفی برای گفتن داشته باشند و عصاره تمام اطلاعات آنها در مدل گرفته شده باشد. بنابراین در نمودارهای AC و PAC هیچ کدام از شاخک ها نباید از محدوده خط نقطه چین بیرون بزند. اگر اینگونه باشد این پیام را دارد که باقیمانده ها خود همبستگی یا خودهمبستگی جزئی ندارند (این به نوعی همان هدف آزمون دوربین واتسون است)
سلام
ببخشید
برا تحلیل سری های زمانی چند متغیره چه جزوه یا کتابی پیشنهاد می کنید؟
میشه از e views استفاده کرد برای این کار؟
سلام؛ فعلا در این زمینه اطلاعات زیادی ندارم و کار نکردم.
البته سری زمانی یک متغیره را به خوبی با ایویوز می شود تحلیل کرد.
سلام…خسته نباشید
نتیجه ازمون دوربین واتسون مدل من 1.28 بدست امده است. داده ی پرتی هم در داده ها وجود ندارد.
امکانش هست که برای رفع این مشکل راهنمایی بفرمایید؟
سلام؛ این مقدار دوربین واتسون 1.28 نشان می دهدکه باقیماندهای مدل شما با یکدیگر خود همبستگی دارند.
یکی از راههای اصلاح این است که متغیر AR(1) را در سمت راست رگرسیون خود وارد و مدل را مجدد ران کنید
سلام. وقت بخیر.
برای محاسبه بازه آماره دوربین- واتسون، هنگامی که n خیلی بزرگ هست چه کاری باید انجام داد؟ اکثر جداول این آماره، تا n=200 بیشتر ندارند. من دیتام روزانه هست و حدودا 2000 تا مشاهده دارم.
سلام؛ برای خود من خیلی کم پیش آمده که از جدول دوربین واتسون استفاده کنم و همینکه می بینم مقدار این آماره در بازه 1.5 تا 2.5 است، نتیجه می گیرم که بابت خود همبستگی بین باقیمانده ها مساله خاصی وجود ندارد. مگر اینکه متوجه رفتار خاصی در باقیمانده ها شوم.
شما هم اگر حساسیت خاصی وجود ندارد، به همین صورت اقدام نمایید. این تعداد داده زیادی که شما دارید، خود به خود دقت برآوردها را بالا می برد.
در عین حال پاسخ سوال شما به نظر من این است که حالت بیشترین یعنی n=200 را ملاک عمل قرار دهید.
بسیار سپاسگزارم از توضیحات و راهنمایی شما.
در آزمون دوربین وانسون n نباید کمتر از ۱۵ و بیشتر از ۱۰۰ باشد(بیشتر از ۱۰۰سال نداریم)همچنین برای ۵ متغیر مستقل تعریف شده نباید بیشتر باشند
سلام وقتتون بخیر
آماره دوربین واتسون مدل من 1.44 به دست آمده و همه داده هامم درست است .
از نظر شما مدل من اشتباه است؟
لطفا راهنماییم کنید
ممنونم
سلام. کمی قضاوت سخت است. با توجه به اینکه عدد کمتر از 1.5 بدست آمده روی مدل باز هم کار کنید و نمودار ACF و PACF باقیمانده ها را ترسیم کنین تا ببینید که آیا واقعا خودهمبستگی دارند یا خیر. یا اینکه مقادیر پرت را در داده ها شناسایی و حذف کنید و دوباره مدل را ران کنید.
البته یک نکته عرض کنم که اگر داده های شما پانل باشد، این مساله قابل چشم پوشی است و من دیده ام در مقالات معتبر که دوربین واتسون کمتر از این هم داشته اند و اقدام خاصی صورت نداده اند.
اگر داده های شما پانل است، این بسته آموزشی را دریافت نمایید: https://www.eviews-iran.ir/product/analysis-goodness-of-fit/
ممنون از راهنماییتون
خیلی لطف کردید.
دانشجوی مهندسی صنایع
سلام وقت شما بخیر
از روی نمودارacf و pacf چطور میشه ایستایی رئ تشخیص داد؟
سلام. این نمودارها را برای متغیر مورد نظر که ترسیم کردید، نباید هیچ کدام خطی داشته باشند که محدوده نقطه چین رد شده باشد.
البته آزمون ریشه واحد در نرم افزار ایویوز به خوبی ایستایی را آزمون می کند و آموزش ویدئویی آنرا با قیمت بسیار ارزانی در منو محصولات همین وب سایت می توانید تهیه کنید
سلام
با تشکر از مطلب بسیار مفیدتون
من مدلی با مشخصات n=38 و k=13 ساخته ام که میزان dL و dU در جدول برای این مدل برابراست با: 0.79583 و 2.35.
آماره d مدل برابر با 2 بدست آمده است. وقتی مقدار dU بیشتر از 2 باشد آیا بدین معنی است که نمی توان درباره هم بستگی باقی مانده ها اظهار نظر کرد؟
سلام. خواهش
عدد دوربین واتسون بدست آمده از مدل شما بین dl و du است و طبق معیار تصمیم گیری نمی شود در خصوص خودهمبستگی باقیمانده های مدل شما نتیجه گیری خاصی کرد. تعداد داده ها با توجه به متغیرهایتان کم است.
از روشهای دیگری مثل ترسیم نمودار acf و pacf باقیمانده ها استفاده نمایید. یا سایر روشهای توضیح داده شده در همین صفحه و دیدگاه های آن.
با سلام و خسته نباشید . یه سوال داشتم در مورد ران مدل نهایی فرضیه ها که با ایویوز انجام میشه وقتی مدل ترکیبی است خواستم بدونم در ایویوز در موقع ران کردن نهایی فرضیه ها کراس سکشن روی چی بزارم؟ نان درسته؟ چون سه گزینه داره ثابت وتصادفی و نان
سلام. این دقیقا همان بخش اصلی و فنی تحلیل داده های ترکیبی یا پانل است. اینکه مدل ما پانل است یا پولد، و اینکه مدل با اثرات ثابت است یا اثرات تصادفی.
برای تشخیص این گزینه های مدل دو آزمون می بایست انجام دهید. لینک آموزش پانل دیتا را ببینید.
در منو محصولات آموزشی فعلا آموزش ران کردن مدل را نداریم اما می توانم فیلم یکی از کلاسهای خصوصی خود را زمانش یک ساعت و ربع است برایتان بفرستم. اگر مایلید در واتس آپ به من پیام دهید (09155136129)
با سلام و خسته نباشید . یه سوال وقتی مدل ترکیبی است و مشکل خود همبستگی هست چه طور در ایویوز رفع کنم؟
سلام. در این خصوص اطلاعات شما که افزایش یابد، مساله حل خواهد شد. این آموزش را از منو محصولات سایت دریافت نمایید:
برطرف کردن موضوع نرمال نبودن داده های پانل- نقض فروض رگرسیون
با سلام و خسته نباشید . یه مقاله مینویسم که تو ران به مشکل برخوردم و ممنون میشم کمکم کنین. یکی در مورد دوربین واتسون هستش که مدل من اثرا ثابت هست و دوربین واتسونم از 2.5 بالاتر هستش که من پارامتر (1)ar را اضافه کردم ولی با این کار دوربین واتسون 2.47 و2.49 شده برا فرضیه هام . میگن مقدار دوربین واتسون باید در بازه 1.5 و 2.15 باشه ولی خب با اضافه کردن این پارامتر یعنی همون (1)ar نزدیک 2.5 شده موردی نداره؟ تو رو خدا کمکم کنین
سلام. در داده های پانل خیلی نگران دوربین واتسون نباشید. دوربین واتسون بین 1.5 تا 2.5 مورد قبول است.
برای اطلاع بیشتر در خصوص پیش فرضهای رگرسیون پانل دیتا، محصول آموزشی نقض فروض رگرسیون در پنل دیتا را دریافت نمایید. این محصول دید شما را بازتر می کند
با سلام یه سوالم دارم در مورد تشخیص الگوی داده پولد و پانل هست که دو تا آزمون براش انجام میشه یکی اف لیمر و دیگری هاسمن هستش که من آزمون بروش پاگان و هاسمن رو برا تشخیص مدل پولد ویا پنل انجام میدم یعنی به ما بروش پاگان و هاسمن رو یاد دادن . شما آموزش تصویری اف لیمر رو دارین بهم یاد بدین کمک بزرگی میکنین ممنون
سلام. اصل سختی کار پانل دیتا همین تشخیص مدل با اثرات ثابت یا مدل با اثرات تصادفی است. و با نشان دادن مسیر آزمون اف لیمر حل نمی شود.
این بسته آموزش ویدئویی را دریافت نمایید تا به خوبی به مقصود برسید:
https://www.eviews-iran.ir/product/f-limer-hausman/
با سلام .ببخشید یه سوال دارم برا خودهمبستگی و رفع آن یکی از آزمونها بریوچ گادفری یا lm هست که من مسیر انجام این آزمون رو از سایت خوندم که از منوی view قسمت residual test و بعد قسمت serial correlation lm test ولی من این مسیر رو از منوی view پیدا نمیکنم میشه مسیرشو بهم بگین اگه هم بسته آموزشی این آزمون رو دارین کدوم بسته آموزشی شما رو باید بخرم و هزینه آن هم بگین و اینکه آیا آزون بریوچ گادفری یا lm برا تشخیص خودهمبستگی و رفع آن در این بسته آموزشی توضیح داده شده اصلا این محصول آموزش رو دارین
سلام. این آموزش: https://www.eviews-iran.ir/product/normality/
و اگر ویدئویی آنرا بخواهید این لینک: https://www.eviews-iran.ir/product/analysis-goodness-of-fit/
با سلام آقای فرشچی برا زمانی که مدل ترکیبی است با اثرات تصادفی یا ثابت و مشکل خودهمبستگی هست چه آزمون هایی برا رفع اون هست من میدونم یکی از روش ها مقدار دوربین واتسون هست که باید در بازه 1.5 تا 2.5 باشد خواستم بدونم به غیر از دوربین واتسون دیگه چه روشی برا رفع خودهمبستگی است وقتی مدل ترکیبی با اثرات ثابت باشه هست؟ و شما برای اون چه بسته بسته آموزشی دارین چون من نمیدونم چه بسته ازشما رو بخرم که رفع مشکل خودهمبستگی برا مدل ترکیبی با رویکرد اثرات ثابت یا تصادفی باشه
سلام. هنگامی که با مساله خودهمبستگی روبرو هستید، آزمون دوربین واتسون هست که اشاره نمودید. راه دیگر محاسبه رگرسیون با استفاده از باقیمانده ها است. راه دیگر ترسیم نمودار acf و pacf باقیمانده ها است.
راه حل : شناسایی و حذف داده های پرت – یا گذاردن متغیر ar(1) در مدل.
سلام و روز بخیر. من یه مشکل دارم ممنون میشم رراهنماییم کنیید.
مدل من اثرات ثابت هست از ازمون براش گادفری استفاده کردم و متوجه شده خودهمبستگی در اجزای اخلال جود داره ، برای رفع اون ar(1) رو در سمت راست مدل اضافه کردم اما بعد از برآرود دیدم که ضریب ar(1) معنی دار نیست، آیا این موضوع اهمیت داره؟
سلام. وقت شما بخیر. مدل من EGLS هست و با AR1 آماره دوربین واتسون مدلم 2.21 هست و با AR2 این آماره 1.23 هست. تو کتاب دکتر سوری هم نوشتن دوربین-واتسون h باید بین 1.96 و -1.96 باشه. اما واقعا کدوم صحیح تره؟ممنون میشم اگه راهنمایی بفرمایین
سلام. با شرایطی که گفتید مدل با AR1 بهتر است. 2.21 برای دوربین واتسون خوب است.
سلام، ببخشید که سئوال متفاوتی دارم.بفرض در Eviewsآزمون ریشه واحد دیکی-فولر را انجام داده ایم .چگونه میتوانیم جدول نتایج را بهمان صورت بر روی دسکتاپ ویا در جایی دیگر کپی نمود ؟ سپاسگزارم
سلام. با انتخاب بخشهای مورد نیاز از خروجی نرم افزار (با کشیدن موس روی خروجی یا select کردن) بعد کپی کردن و سپس پیست کردن در فایل ورد می توانید خروجی نرم افزار را به پایان نامه خود انتقال دهید.
از آموزشهای ویدئویی ما در منو “محصولات آموزشی این سایت” برای یادگیری کار با ایویوز استفاده نمایید.
سلام خسته نباشیدمدل من 2SLS و وقتی مدل را ران میکنم خود دوربین واتسون معادله دوم باAR(1) از 0.5 به 2.92 میرسه و معادله اولم با AR(1) از 0.7به 0.9 میرسه اما PROBها بی معنی میشن ممنون میشم راهنمایی کنید
سلام. روش 2SLS را مسلط نیستم. سایر دوستان اعلام نظر کنند.
سلام اگر بخواهم فرمول دوربین واتسون رو تو نرم افزار r بنویسم و داده وارد کنم چکار باید بکنم لطفا راهنمایی کنید
سلام. با فرمول نویسی در نرم افزار آر آشنایی ندارم.
سلام یک سئوال دارم راههای شناسایی خود همبستگی سریالی و رفع آن چیست
سلام. سوال خیلی کلی است. برای رفع خودهمبستگی سریالی و آشنایی کامل با آن به سراغ منو محصولات بروید و محصول (شناسایی و رفع نرمال نبودن داده ها و خودهمبستگی ) را خریداری نمایید.
سلام در منابع خوندم که اگر در سمت راست متغیر با وقفه وجود داشته باشد نمیتوان از دوربین واتسون استفاده کرد …در مدل هایی که با gls ساخته میشوند به جای دوربین واتسون میتوانم از ازمون بریوش گادفری استفاده کنم؟
با سلام چند سوال داشتم.
1- داده های پرت زیاد دارم. زمانی که داده ها وارد نرم افزار میشوند با trimming دادهای پرت را حذف کردم اما بازهم نرمال نیستندبرای نرمال کردن یا اصلاح کردن متغیرها قبل از ورود به نرم افزار از چه روشی استفاده کنم؟
2- در یکی از فرضیه هایم اثرات ثابت است و مشکل خود همبستگی دارد برای رفع آن از (1)ar استفاده کردم اما خطای نزدیک به ماتریس واحد را می دهد
3-داده ها از نوع پانل هستند برای بررسی فروض کلاسیک مثلا نا همسانی وایانس در مدل پانل از چه آزمونی استفاده کنم (ازمون وایت در پانل جواب نمیدهد)
سوالی از stata دارم برای بررسی ناهمسانی واریانس زمانی که اخرین دستور Lrtest hetero hemo, df (`df’)را وارد میکنم خطا می دهد که hemo را نمی شناسد یا برای آزمون نرمال بودن باقیمانده آخرین دستور خطای میدهد که jarque-bera را نمیشناسد چطور میتوانم مشکل را برطرف کنم
ممنون میشوم راهنمایی بفرمایید و اینکه از کدام محصول آموزشی استفاده کنم.
سلام. 1- در داده های پانل قرار نیست متغیرها نرمال شوند. حتی می توان از نرمال شدن باقیمانده های مدل چشم پوشی کرد. از منو محصولات “شناسایی و رفع نرمال نبودن و ناهمسانی واریانس” را دریافت نمایید. 2- مساله خود همبستگی نیز تا حدی مانند نرمالیتی قابل اغماض است. مقالاتی معتبر دیده ام که آماره دوربین واتسون آن 1.4 بوده است. 3- اینکه چطور در داده های پانل ناهمسانی واریانس را بررسی کنید محصول آموزشی ذکر شده در بند 1 را دریافت نمایید. 4- در خصوص استتا اطلاعات زیادی نداریم و در این سایت بر ایویوز تمرکز کرده ایم.
با سلام و خسته نباشید
من مدل پنل با اتراث ثابت یک طرف در مقطع را تخمین زدم ولی متاسفانه بعضی از پراب ها در سطح 5 درصد معنادار نمی باشد.
لطفا راهنمایی فرمائید. باتشکر
سلام. آیا بررسی و کنترل داده های پرت را انجام داده اید؟ یک آموزش در این خصوص در منو محصولات هست. گاهی یک داده پرت سرنوشت یک پراب را تغییر می دهد!
خیلی ممنون و متشکرم بابت توضیحات ساده و روان
سلام ..میتونید یک توضیح خلاصه اینکه اماره دوربیت واتسون 2.17 است یعنی چه
سلام. اینکه این عدد نزدیک به عدد 2 است، خیلی خوبه و نشان دهنده این است که خودهمبستگی در جملات خطا (باقیمانده ها) وجود ندارد.
سلام
میخواستم بدونم دلیل اینکه میگن در خود همبستگی با کواریانس مثبت، واریانس کم میشه چیه؟
و چرا با کواریانس منفی، واریانس بیشتر میشه؟